前置
先来定义形式幂级数,为一个形如 \(\sum_{n\ge0}a_nx^n\) 的表达式。
其中, \(x^n\) 为占位符,没有类似于自变量一样的实际含义。
\(\{a_i\}\) 是系数序列,实际上,你完全可以将这个形式幂级数看做数列的一种写法。
举个例子, \(f(x)=1+x+x^2+\cdots x^n\), \(g(x)=1-x+x^2-x^3+\cdots (-1)^{n+1}x^n\) 都是形式幂级数。
多项式可以看做形式幂级数的子集,只有有限项。
记 \([x^n]f(x)\) 为 \(f(x)=\sum_{n\ge0}a_nx^n\) 第 \(n\) 项系数 \(a_n\) 。
声明
下面所有内容并不保证十分严谨,仅适合初学者了解。
并不会解释诸如形式幂级数收不收敛,为什么占位符被当做变量一样的问题。
诸如这是定义在一个环上的运算之类的作者并不会。
我们希望通过形式幂级数的封闭形式来获得原问题的一种计算方式。
记数列 \(\{a_n\}\) 的对应形式幂级数为 \(A(x)\) , \(\times\) 表示卷积。
下面可能会将形式幂级数看做变量或多项式处理,并不会严谨证明,人是无法说出自己并不了解的事情的。
普通生成函数(OGF)
记 \(f(x)=\sum_{n\ge0}a_nx^n\) 为数列 \(\{a_n\}\) 的普通生成函数 \((OGF)\) 。
容易发现,如果 \(c_n=\sum_{i=0}^{n}a_i b_{n-i}\) ,那么 \(C(x)=A(x)\times B(x)\) 。
一些常用的 \(OGF\) 如下:
(建议记住)
上面两个式子的证明只需要把右侧分母乘过来,然后发现确实成立。
组合意义为,从若干组中无序选出若干个元素。
举个例子才能更好地理解这个有什么用。
应用
求解线性递推通项公式
举个例子,数列的前两项为 \(f_0, f_1\) ,对于 \(n\ge 2\) , \(f_n=2f_{n-1}+3f_{n-2}\) 。
求通项公式。
记 \(F(x)=\sum_{n\ge0}f_nx^n\) ,
则有:
移项化简得:
令 \(A(1-3x)+B(1+x)=f_0+(f_1-2f_0)x\) ,解得 :
又根据
所以, \([x^n]=(-1)^nA + 3^nB\) 。
维护方案数
分组
有 \(k\) 个集合,从第 \(i\) 个集合中选出 \(k\) 个物品的贡献为 \(v_{i,j}\) 。
则第 \(i\) 个集合的 \(OGF\) 为 \(F_i(x)=\sum_{k\ge0}v_{i,k}x^k\) 。
总共选出 \(n\) 个元素的所有方案总贡献为 \([x^n]\prod_{i}F_i(x)\) 。
背包
每个物品看做一组。
记 \(f_n=\text{选出重量恰好为 n 的方案数}\) 。
那么,每件物品的 \(OGF\) 为 \(F_i(x)=1+x^{w_i}\) 。
那么,总方案数就是 \([x^W]\prod_{i}F_i(x)\) 。
抽奖机
(无题源)
每次按下抽奖机按钮,有 \(p\) 的概率弹出一个彩蛋, \(1-p\) 的概率关机,每个彩蛋有 \(\frac{1}{2}\) 的概率中奖,获得一个奖品。
问抽奖机关机时,恰好获得 \(k\) 个奖品的概率。
点击查看
推式子:
P10780 BZOJ3028 食物
求 \(\boldsymbol{无序选出}\) \(n\) 个食物的方案数。
点击查看
设 \(f_x\) 表示某种食物选择 \(x\) 个的方案数。
记 \(F(x)=\sum_{n\ge 0}f_nx^n\) 。
则 \(ans=[x^n]\Pi F_c(x)\)
下面写出每种食物对应的 \(F(x)\) 。
全部相乘化简得到 \(ans=[x^n]\frac{x}{(1-x)^4}\) 。
根据组合意义插板法得:
P6189 [NOI Online #1 入门组] 跑步
求将一个正整数 \(n\) 划分成若干个正整数之和的方案数。
(我们只关心划分成了哪些数,而不关心它们的顺序)
点击查看
先来介绍一些前置知识。
- (广义)五边形数
下图是五边形数。
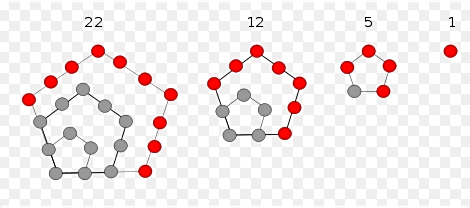
(图片来自百度)
容易发现通项公式, \(f(n)=\frac{3n^2-n}{2}\) 。
下面来介绍广义五边形数,就是将 \(0,1,-1,2,-2\cdots\) 依次代入上式后得到的数列:
我们用 \(p_n\) 表示。
- 欧拉函数(不是数论里那个)
- 五边形数定理
发现 \(x\) 的指数上就是我们刚才定义的广义五边形数,定理名由此而来。
这定理第一次由欧拉证明。
下面来求解问题。
记 \(f(n)\) 为将 \(n\) 拆分成正整数之和的方案数。
所以我们需要求解 \(\phi(x)\) 的逆,可以当做多项式来求逆。
因为常数项为 \(1\) ,所以逆的常数项为 \(1\) 。
然后,从低到高确定每一位的系数,具体地,只需要将次数更低的结果算出来取负即可。
因为 \(\phi(x)\) 的指数 \(O(n^2)\) 级别的,所以 \(phi(x)\) 只有 \(O(\sqrt n)\) 项系数非负。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)const int _ = 2e5 + 7;
typedef long long ll;ll n, mod, p[_];ll _5(ll k) { return (3 * k * k - k) / 2; }int main() {scanf("%lld%lld", & n, & mod);p[0] = 1;lep(i, 1, n) {int j = 0, op = 1;while (++j) {int x = _5(j), y = _5(-j);if (x <= i) p[i] = (p[i] + op * p[i - x]) % mod;if (y <= i) p[i] = (p[i] + op * p[i - y]) % mod;if (x > i or y > i) break; op *= -1;}}p[n] = (p[n] + mod) % mod;printf("%lld\n", p[n]);return 0;
}
指数生成函数 (EGF)
记 \(f(x)=\sum_{n\ge0}\frac{a_n}{n!}x^n\) 为数列 \(\{a_n\}\) 的指数生成函数 \((EGF)\) 。
当 \(c_n=\binom{n}{i}a_ib_{n-i}\) 时满足 \(C(x)=A(x)\times B(x)\) 。
容易验证:
组合意义为,从若干组中选出若干个元素并有序排列。
容易发现, \(\binom{n}{i}\) 是在给 \(A\) 中的元素选择位置。
在这里指出两个函数的幂级数:
应用
分组
有 \(k\) 个集合,从第 \(i\) 个集合中选出 \(k\) 个物品的贡献为 \(v_{i,j}\) 。
则第 \(i\) 个集合的 \(EGF\) 为 \(F_i(x)=\sum_{k\ge0}\frac{v_{i,k}}{k!}x^k\) 。
总共选出 \(n\) 个元素并有序排列的所有方案总贡献为 \(n![x^n]\prod_{i}F_i(x)\) 。
错位排序
满足 \(\forall\) \(i\) , \(i\ne p_i\) 的排列 \(p\) 的个数。
点击查看
错位排序可以看做若干个置换环。
每个大小为 \(c\) 的置换环贡献为 \((c-1)!\) 。
(其实就是环排列)
定义每个环的 \(EGF\) 为 \(F(x)=\sum_{c\ge 2}\frac{(c-1)!}{c!}x^c=\sum_{c\ge 2}\frac{1}{c}x^c\) 。
进一步化简得到:
所以:
相当于 \(e^{-x}\) 的系数前 \(n\) 项做前缀和后再乘 \(n!\) 。
容易发现这就是错位排列的通项公式:
Chocolate
将长度为 \(n\) 的序列染上 \(c\) 种颜色,恰好有 \(m\) 种颜色出现奇数次的概率。
点击查看
记某种颜色出现奇数次的 \(EGF\) 为 \(O(x)\) ,出现偶数次的 \(EGF\) 为 \(E(x)\) 。
则
\(O(c^2)\) 暴力计算即可。

 OGF + EGF
OGF + EGF